LeetCode刷题(19)【简单】二叉树的前&&中&&后序遍历(C++)

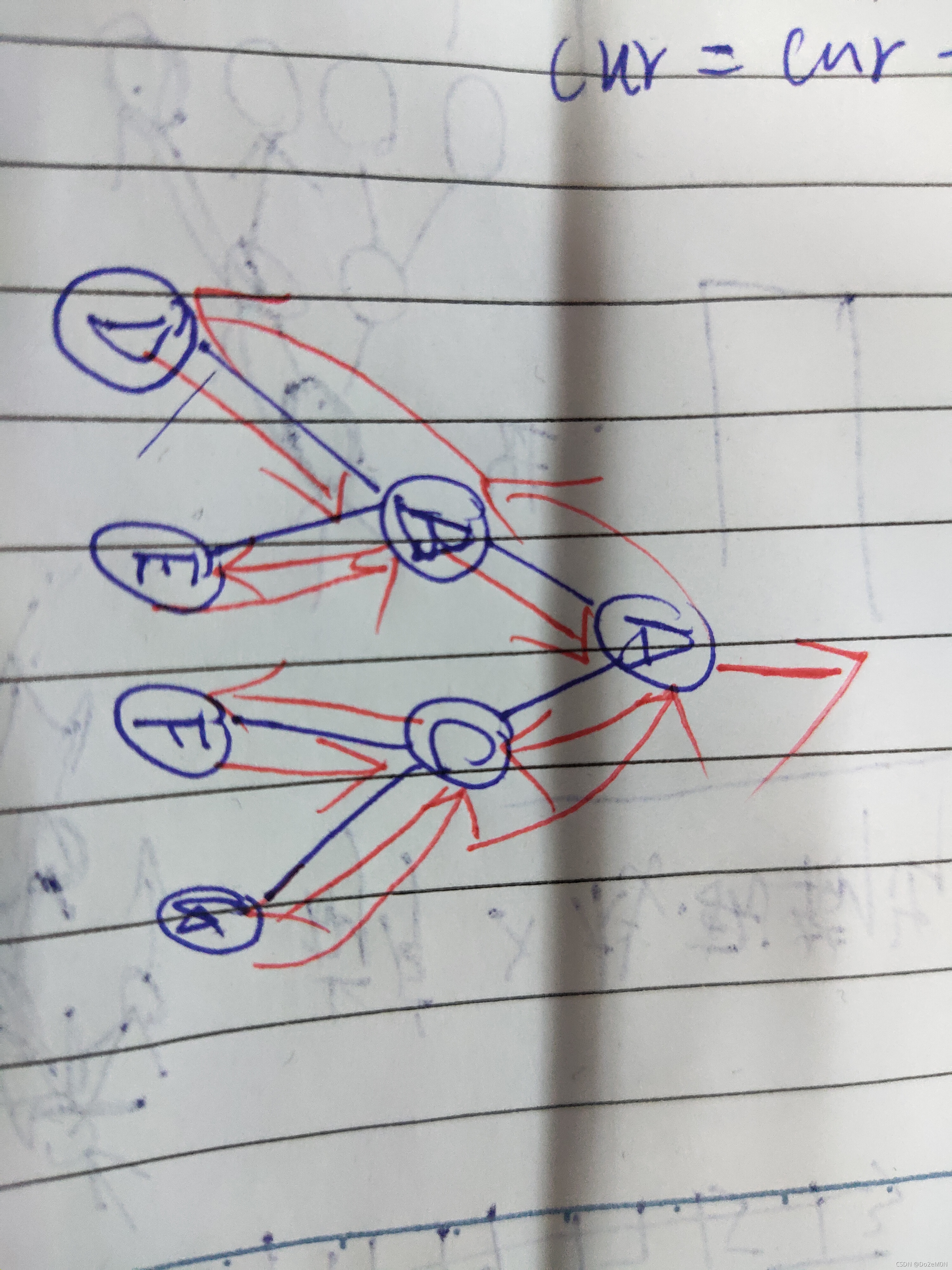
精华在于进栈和出栈的时机

94.二叉树的中序遍历

题目

思路：
中序遍历的顺序是，左 - 根 - 右
创建一个栈来存储结点，创建一个vector来存储中序遍历的值
从根结点开始，只要该结点有左子树，就将该结点压进栈中。
直到root为空。
取出栈顶元素，栈顶元素出栈，将该结点值存进recv。
…
剩下的只可意会不可言传了，

感谢这位老哥分享——链接

class Solution {
public:
    //中序遍历顺序-左-中-右
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>recv;
        stack<TreeNode*> Tstack;
       
       //当前结点不为空或当前栈不为空
       while(root || !Tstack.empty())
       {
           while(root)
           {
               //只要当前结点不为空就往栈里面压
               Tstack.push(root);
               root = root->left;
           }
           //此时栈顶元素为根节点左侧树最左的左子树
           //取到该结点
           root = Tstack.top();
           Tstack.pop();
           //pop出栈，存进recv中
           recv.push_back(root->val);
           root = root->right;
       }
        return recv;
    }
};

递归方法

144.二叉树的前序遍历

题目

非递归
感谢这位老哥分享——链接

class Solution {
public:
    
    vector<int> preorderTraversal(TreeNode* root) {
    vector<int>recv;
    stack<TreeNode*>Tstack;
    while(root || !Tstack.empty())
    {
        while(root)
        {
            recv.push_back(root->val);
            Tstack.push(root);
            root = root->left;
        }
        root = Tstack.top();
        Tstack.pop();
        root = root->right;
    }    
    return recv;
    }
};

145.二叉树的后序遍历

题目

一直往栈里面往左节点，压到左边最后一个做结点，往回pop,判断当前这个结点是否右结点，有右结点就输出，最后判断自己。

感谢这位老哥分享思路—链接

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int>result;
        stack<TreeNode*>Tstack;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;//记录cur上一个指向的结点，比cur走慢一步

        while(!Tstack.empty() || cur)
        {
            //只有cur不为空，就一直往里面压左节点
            while(cur) 
            {
                Tstack.push(cur);
                cur =cur->left;
            }
            cur = Tstack.top();
            //如果当前结点没有右结点 ||  右结点已经访问过了
            if(!cur->right || prev == cur->right)
            {
                Tstack.pop();
                result.push_back(cur->val);
                prev = cur;
                //要从栈里面往外面吐结点，所以要将cur置为null
                cur = nullptr;
            }   
            else
            {
                cur = cur->right;
            }
        }
        return   result;
    }
};

大致流程感觉