单链表存在的缺陷:
不能从后往前走,
找不到他的前驱,
指定位置 删除 增加 尾删 都要找前一个,时间复杂度都是O(n)
针对上面的这些缺陷的解决方案——双向链表。
实际中要实现的链表的结构非常多样,以下情况组合起来就有8种链表结构:
- 单向、双向
- 带头、不带头——带哨兵位的头结点,这个结点不存储有效数据,好处是什么?尾插的判断更方便简单,带头就不需要二级指针了,(带头结点,不需要改变穿过来的指针,也就是意味着不需要传二级指针了。)
- 循环、非循环
- 无头单向非循环:结构简单,一般不会单独用来存数据,实际中更多是作为其他数据结构的子结构,如哈希桶,图的邻接表等,另外这种数据结构在笔试面试中出现很多。
- 带头双向循环链表:结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构,都是带头循环双向链表,另外,这个结构虽然复杂,但是使用代码代码实现的以后会发现结构带来许多优势,实现反而简单了。
带头双向循环链表
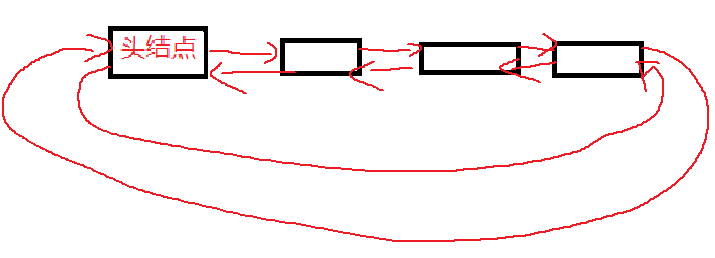
结构体创建
结构体创建:
1
2
3
4
5
6
7
| typedef int LSTNodeData;
typedef struct ListNode
{
LSTNodeData data;
struct ListNode* next;
struct ListNode* prev;
}LSTNode;
|
创建结点
创建结点:
1
2
3
4
5
6
7
8
| DBLSTNode* DBLSTCreat(DoubleListDataType x)
{
DBLSTNode* newnode = (DBLSTNode*)malloc(sizeof(DBLSTNode));
newnode->data = x;
newnode->next = NULL;
newnode->prev = NULL;
return newnode;
}
|
初始化
初始化:
有个小哨兵位的头结点,并且是一个循环状态。
1
2
3
4
5
6
7
8
9
| DBLSTNode* DBLSTInit()
{
DBLSTNode* phead = DBLSTCreat(0);
phead->next = phead;
phead->prev = phead;
return phead;
}
|
销毁
销毁:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void DBLSTDestory(DBLSTNode* phead)
{
DBLSTNode* cur = phead->next;
while (cur !=phead)
{
DBLSTNode* curNext = cur->next;
free(cur);
cur = curNext;
}
free(phead);
}
|
画图有利于双向链表的理解。
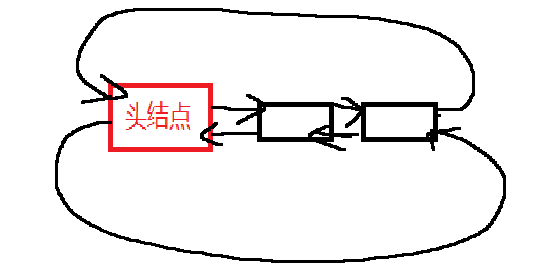
打印
打印:
1
2
3
4
5
6
7
8
9
10
11
12
| void DBLSTPrint(DBLSTNode* phead)
{
DBLSTNode* cur = phead->next;
while (cur != phead)
{
printf("%d ", cur->data);
cur = cur->next;
}
printf("\n");
}
|
尾插
尾插:
双向带头循环链表,结构虽然复杂了,但是更容易操作了。
这就是结构设计的优势。
1
2
3
4
5
6
7
8
9
10
11
12
| void DBLSTPushBack(DBLSTNode* phead, DoubleListDataType x)
{
DBLSTNode* newnode = DBLSTCreat(x);
DBLSTNode* tail = phead->prev;
tail->next = newnode;
newnode->prev = tail;
newnode->next = phead;
phead->prev = newnode;
}
|
头插
头插:
如果插入的时候链表是空的同样不会有影响。
有first这几个指针先动谁都行,没有first也可以,就是会有顺序要求。
示例:
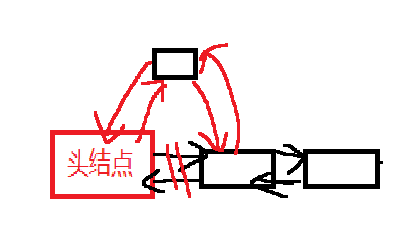
1
2
3
4
| newnode->next = phead->next;
phead->next->prev = newnode;
phead->next = newnode;
newnode->prev = phead;
|
1
2
3
4
5
6
7
8
9
10
11
12
| void DBLSTPushFront(DBLSTNode* phead,DoubleListDataType x)
{
DBLSTNode* newnode = DBLSTCreat(x);
DBLSTNode* first = phead->next;
phead->next = newnode;
newnode->prev = phead;
newnode->next = first;
first->prev = newnode;
}
|
头删
头删:
1
2
3
4
5
6
7
8
9
10
| void DBLSTPopFront(DBLSTNode* phead)
{
DBLSTNode* first = phead->next;
DBLSTNode* second = first->next;
phead->next = second;
second->prev = phead;
free(first);
first = NULL;
}
|
尾删
尾删:
1
2
3
4
5
6
7
8
9
10
11
| void DBLSTPopBack(DBLSTNode* phead)
{
DBLSTNode* tail = phead->prev;
DBLSTNode* tailPrev = tail->prev;
tailPrev->next = phead;
phead->prev = tailPrev;
free(tail);
tail = NULL;
}
|
查找位置
查找位置:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| DBLSTNode* DBLSTFind(DBLSTNode* phead,DoubleListDataType x)
{
DBLSTNode* cur = phead->next;
while (cur != phead)
{
if (cur->data == x)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
|
使用:
1
2
3
4
5
6
7
8
9
| DBLSTNode* pos = DBLSTFind(phead,x);
if(pos)
{
printf("找到了");
}
else
{
printf("没找到");
}
|
删除pos位置的值
删除pos位置的值:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void DBLSTErase(DBLSTNode* pos)
{
DBLSTNode* posPrev = pos->prev;
DBLSTNode* posNext = pos->next;
posPrev->next = posNext;
posNext->prev = posPrev;
free(pos);
pos = NULL;
}
|
在pos前插入x
在pos前插入x:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void DBLSTInsert(DBLSTNode* pos, DoubleListDataType x)
{
DBLSTNode* posPrev = pos->prev;
DBLSTNode* newnode = DBLSTCreat(x);
newnode->data = x;
newnode->prev = posPrev;
posPrev->next = newnode;
newnode->next = pos;
pos->prev = newnode;
}
|
返回链表的结点数量
返回链表的结点数量:
1
2
3
4
5
6
7
8
9
10
11
12
| int DBLSTSize(DBLSTNode* phead)
{
int count = 0;
DBLSTNode* cur = phead->next;
while (cur != phead)
{
count++;
cur = cur->next;
}
return count;
}
|
判断链表是否为空
判断链表是否为空:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| bool DBLSTEmpty(DBLSTNode* phead)
{
DBLSTNode* cur = phead->next;
if (phead == cur)
{
return true;
}
else
{
return false;
}
}
|
优化
为了更快的实现一个双向循环的带头链表,我们可以直接利用Insert和Erase。
如果Erase的pos位置是第一个结点,那就代表着头删,如图:
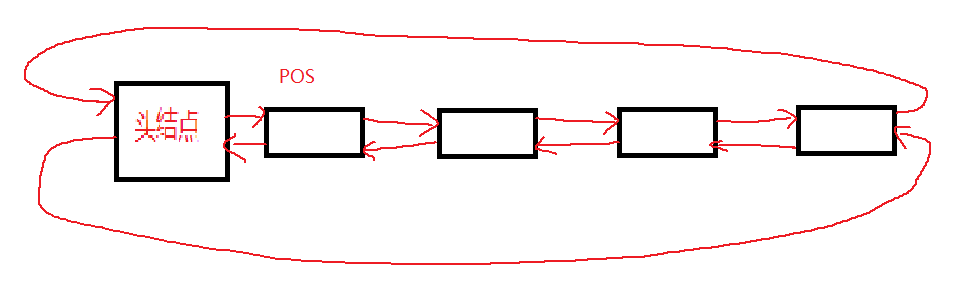
所以头删还可以这样写:
1
2
3
4
| void DBLSTPopFront(DBLSTNode* phead)
{
DBLSTErase(phead->next);
}
|
尾删同理:
1
2
3
4
| void DBLSTPopBack(DBLSTNode* phead)
{
DBLSTErase(phead->prev);
}
|
头插:
1
2
3
4
| void DBLSTPushFront(DBLSTNode* phead,DoubleListDataType x)
{
DBLSTInsert(phead->next,x);
}
|
尾插:
其实就是插到头结点phead的前面。
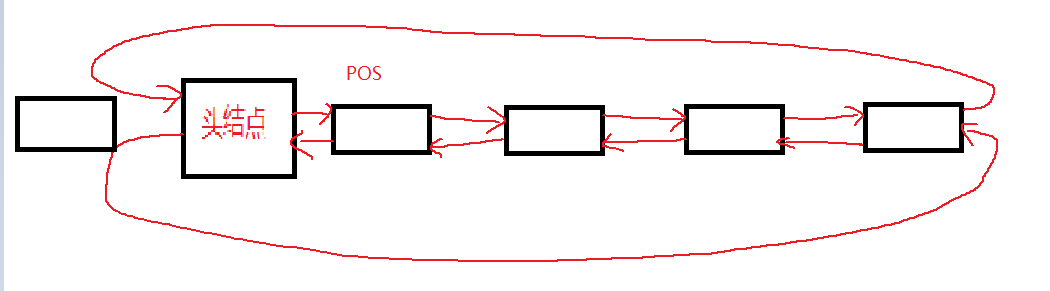
1
2
3
4
| void DBLSTPushBack(DBLSTNode* phead, DoubleListDataType x)
{
DBLSTInsert(phead, x);
}
|
总结
带头双向循环链表,任意位置插入和删除数据,时间复杂度都是O(1)。
查找最优的结构不是这个,查找就得遍历,时间复杂度还是O(N)。
查找的最优结构有三种:
- 平衡搜索树(AVL树和红黑树)
- 哈希表
- B树 & B+树系列 (数据库底层核心引擎)









