认识各种图

相关书籍——《大话数据结构》

图按照有无方向分为无向图和有向图。
- 无向图由定点和边构成。
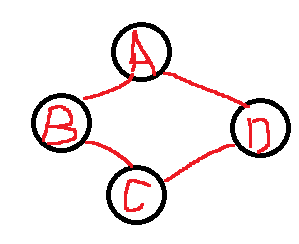
- 有向图由定点和弧构成，弧有弧尾和弧头之分。
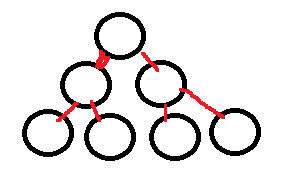
如果任意两个顶点之间都存在边叫做完全图。
- 无向的叫做无向完全图。
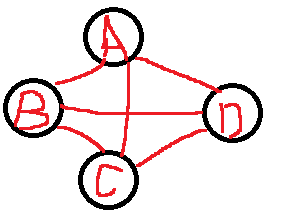
- 有向的叫做有向完全图。
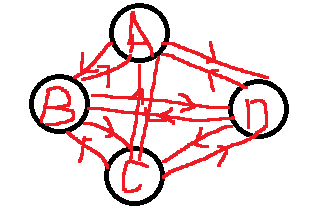
图按照边或弧的多少分为稀疏图和稠密图。
- 都是相对而言的多少。
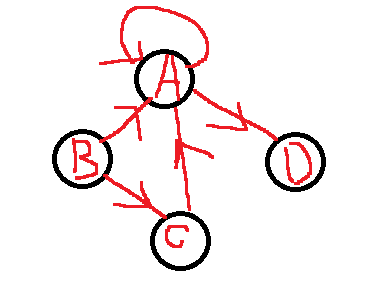
若无重复的变到自身的边叫做简单图。

反例：下面这两个图都不是简单图。
图和顶点之间有邻接点、依附的概念。
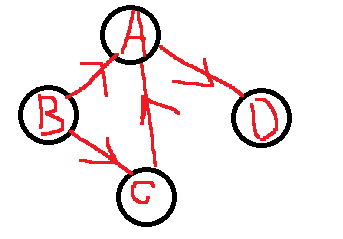
无向图顶点的边数叫做度，有向图顶点分入度和出度。

（入度：有几个箭头指向这个顶点，出度：指向几个顶点。）
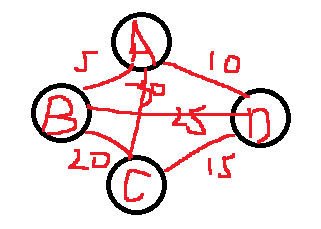
图上的边或弧上带权则称为网。

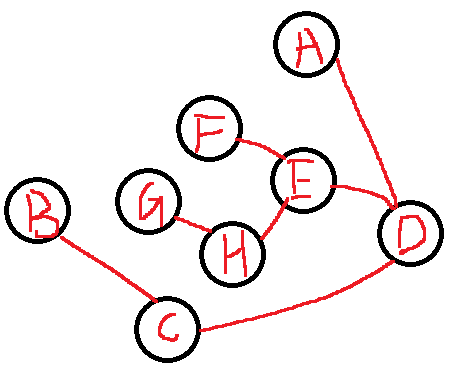
图中顶点间存在路径，两顶点存在路径则说明是连通的。
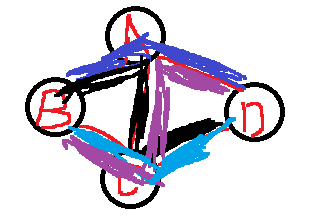
- 例如：由B到D在无向图上有四种不同的路径。
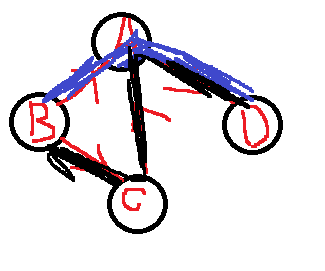
在有向图上由B到D有两种路径。

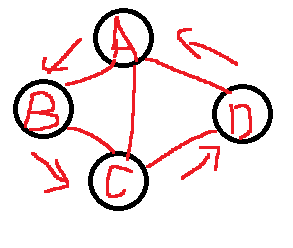
如果路径最终回到起始点则称为环，当中不重复叫简单环。
- 简单环
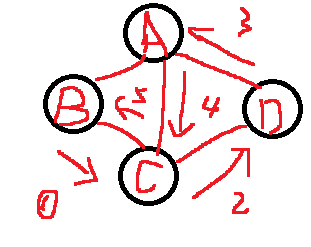
- 不是简单环，顶点C重复了。
若任意两顶点都是连通的，则图就是连通图。
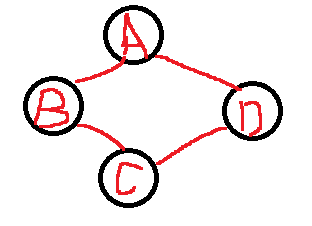
- 不连通图
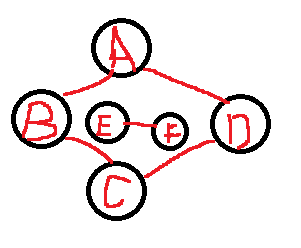
- 有向则称为强连通图。
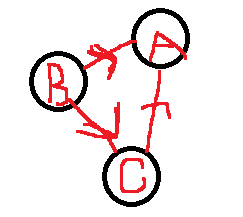
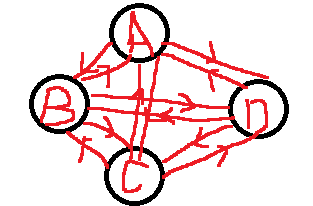
（结合上面的有向完全图，我们不难发现，有向完全图就是强连通图，因为它任意两个定点间都有是连通的，但是强连通图不一定是有完全向图，因为有向完全图需要任意两个顶点间有相反的两条路径。）
- 连通分量强调：
  - 要是子图；
  - 子图是连通的；
  - 连通子图含有极大顶点数；极大顶点数就是最大连通子图上的顶点数量。
  - 具有极大顶点数的连通子图包含依附于这些顶点的所有边。
- 无向图中的极大连通子图称为连通分量，有向的则称为强连通分量。
  - 非连通图的连通分量。
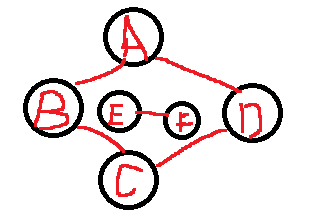
  它的连通分量
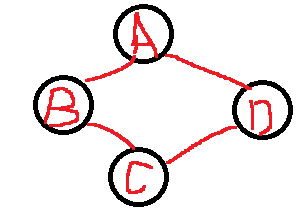
  - 有向但是非强连通图的(极大)强连通分量。
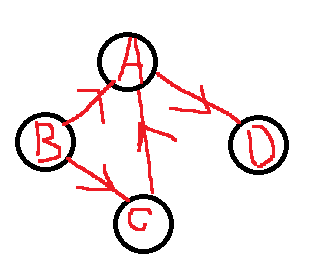
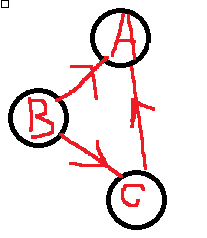
  它的强连通分量。
连通生成树。
- 所谓的连通图的生成树是一个极小的连通子图，它含有图中全部的n个顶点，但只有足以构成一个树的n-1条边。
- 无向图的连通生成树。
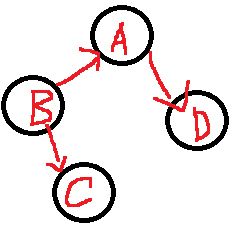
- 有向图恰有一个顶点的入度为0，其余顶点的入度为1，则是一棵有向树。
  
  例如下面这两棵有向树。
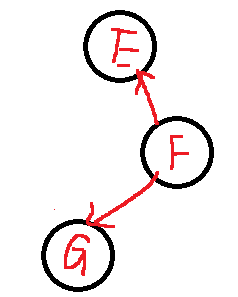
一个有向图由若干棵有向树构成生成森林。
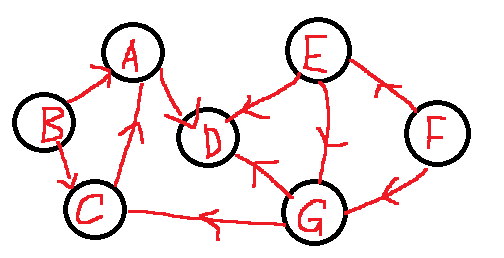
- 一个有向图的生成森林由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧
- 例如：一下三张图，图1是一棵有向图。去掉一些弧之后，它可以分解为两课有向树，如图2和图3，这两棵就是图1有向图的生成森林。