1.二叉树的种类

1.满二叉树:

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树叫做满二叉树。
结点数量2^k-1

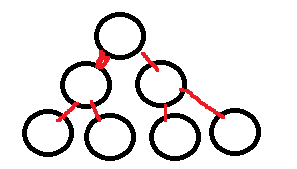
2.完全二叉树

除了底层以外，其它层都是满的，底层是从左到右连续的。
这个是二叉树
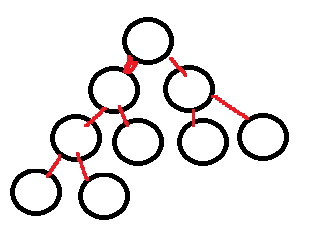
这个就不是二叉树，底层不连续。

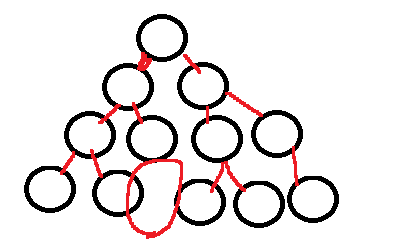
满二叉树一定是一棵完全二叉树，但完全而二叉树不一定是满的。

3.二叉搜索树

在它里面的结点顺序，左子树的所有结点都小于中间结点，右子树的所有结点都大于中间结点。
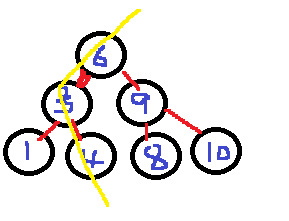
二叉搜索树对结点的布局是没有要求的，元素有顺序就可以。
平衡二叉搜索树
- 左子树和右子树的高度差不能超过1。

2.二叉树的存储方式

1.顺序存储

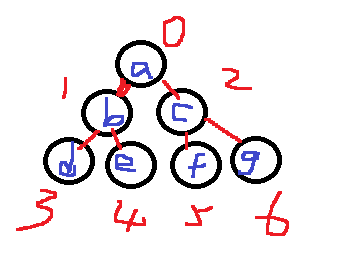
用这个字符数组来保存二叉树。

*2i+1——左孩子，2 i+2——右孩子。*

2.链式存储

一般用的都是链式存储。

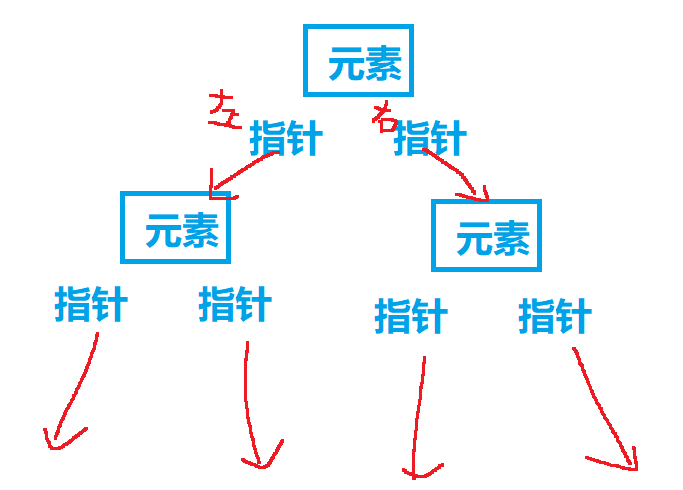
3.二叉树的遍历

扩展：

深度优先搜索：一般都是用递归的方式来实现的，前序遍历，中序遍历，后序遍历，都是深度优先搜索。(迭代法也可以实现前中后序，非递归的方式。)
广度优先搜索：一层一层的去遍历，或者是一圈一圈的去遍历。层序遍历就是广度优先搜索的一种。

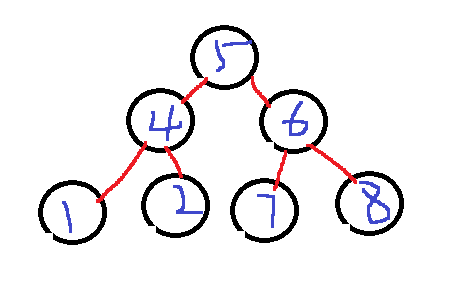
前序遍历：中左右。5412678

中序遍历：左中右。4125768

后序遍历：左右中。1247865

4.二叉树结点的定义

将二叉树理解为一个链表就会简单很多。

struct TreeNode
{
   int val;//放数值
   TreeNode* left;
   TreeNode* right;
    //实现一个构造函数，在new一个结点的时候，方便对其进行初始化。
   TreeNode(t):val:t,left(NULL),right(NULL);	
}